The USA Ultimate algorithm isn't perfect; here's another way.
September 3, 2015 by Wally Kwong in Analysis with 28 comments
Among other sports, I’m a fan of college hockey. And, surprisingly, college hockey shares many of the same issues as ultimate when determining postseason bids: each conference receives one automatic bid, and mathematical formulas1 are used to determine the other 12 teams.2
College hockey also suffers from one of the main problems that plagues ultimate algorithms: a lack of interconnectivity between teams. So I decided to look at the formulas and ranking system adopted in NCAA hockey and seeing if they can be used to improve ultimate rankings.
Methodology
One of the college hockey formulas, the Bradley-Terry system, is based on a stipulation that the probability of a team with rating A defeating a team with rating B is given by A / (A + B).
For example, NationalsTeam has a rating of 4.2. SectionalsTeam has a rating of 0.8. The likelihood of NationalsTeam beating SectionalsTeam is 4.2 / (4.2 + 0.8) = 0.84, or 84%.
But how do we figure out a rating for a single team? Let’s say we have two teams with “known” ratings: RegionalsTeam rated 1.7 and SectionalsTeam rated 0.8. We are trying to figure out the rating for UnknownTeam, which has a 2-3 record against RegionalsTeam and a 2-1 record against SectionalsTeam. We’ll guess an initial rating of 1.0 for UnknownTeam. Using this rating with the Bradley-Terry equation, in the 5 games against RegionalsTeam and 3 games against SectionalsTeam we would expect a win total of:
5 * 1.0 / (1.0 + 1.7) + 3 * 1.0 / (1.0 + 0.8)
which comes out to 3.52 games.
The fact that, in reality, UnknownTeam won a total of 4 games (instead of 3.52) means the rating for UnknownTeam needs to be adjusted up a little bit.3 Using the new adjusted rating, we can again calculate the expected wins of UnknownTeam, and then adjust the rating again.
This enables us to calculate the rating for a single team, but we aren’t adjusting ratings for RegionalsTeam and SectionalsTeam — in the example above, those ratings are held constant. To simultaneously generate ratings for all teams playing during the regular season, I followed this process:
- Give every team an initial estimated rating of 1.0.
- Using current estimated team ratings, calculate adjustments for each team using their win-loss record.4
- Apply the calculated ratings adjustments for each team to generate new estimated ratings.
- Repeat steps 2-3 until the maximum adjustment is tiny5
My initial attempt generated rankings which made no sense: undefeated teams were rewarded way too much, even when using methods to account for this weakness.
However, ultimate has an aspect that can be leveraged to generate a larger data set. Each point of a game can be considered its own “mini-game.” So if a game finished with a score of 15-8, this would count as 23 “mini-games.” Now we’ve got a far larger data set to evaluate. A team’s rating under this system is no longer related to the likelihood of winning an entire ultimate game, but the likelihood of them winning any given point in a game.
2015 College
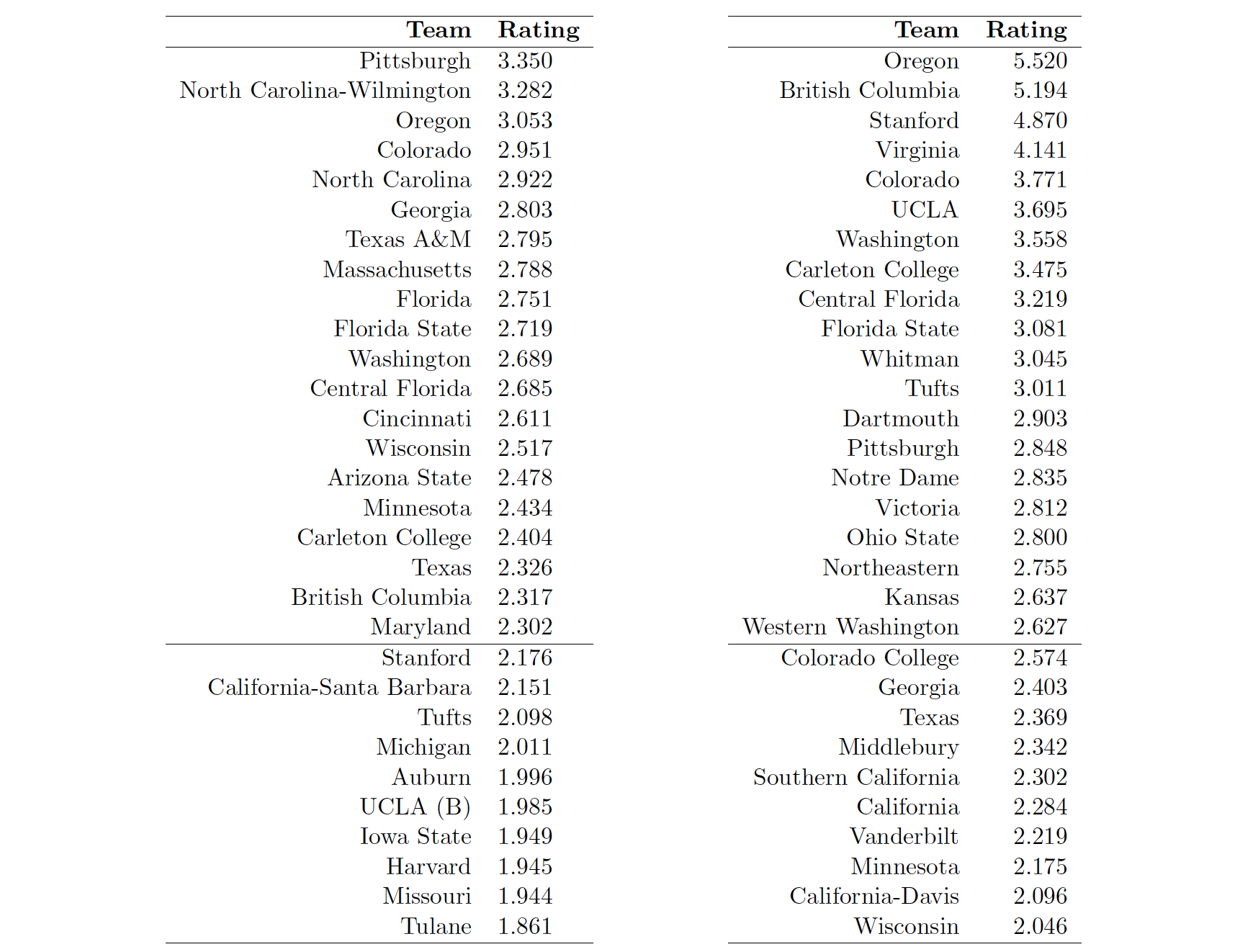
Using this “per-point” method, the 2015 USAU college regular season6 gives the following ratings (Men’s on left, Women’s on right):
Using the above ratings to determine bids to 2015 College Nationals would result in fairly similar results to the actual allotted bids under the USAU algorithm.
On the Men’s side, the sole difference is the strength bid awarded to Maryland and the Atlantic Coast region under the current USAU algorithm is instead awarded to Minnesota and the North Central region. Cincinnati would still have earned its strength bid for the Ohio Valley region.
On the Women’s side, one of the strength bids awarded by the current USAU algorithm to the South Central region is shifted to the Northeast region via Northeastern. The question of which South Central team “lost” the bid is up for debate; in the USAU rankings, Colorado College is ranked above Kansas, while the opposite is true if the above rankings are used.
2015 Club
Just for kicks, I’ve included the ratings using the above algorithm as applied to the 2015 USAU club season (using scores posted as of August 24, 2015). The bids would be as follows.
Men’s
1 bid: Northeast
2 bids: Great Lakes, Mid-Atlantic, Northwest, South Central, Southeast, and Southwest
3 bids: North Central
Compared to the actual bids assigned, the Bradley-Terry system would result in the following bid “changes”: NE: -1; SW +1
| Team | Rating | Strength of Schedule |
|---|---|---|
| Revolver | 3.107 | 2.395 |
| Sockeye | 3.058 | 2.307 |
| Machine | 2.913 | 2.372 |
| Doublewide | 2.873 | 2.416 |
| Truck Stop | 2.857 | 2.503 |
| High Five | 2.799 | 2.512 |
| Johnny Bravo | 2.760 | 2.418 |
| Patrol | 2.650 | 1.768 |
| Madison Club | 2.556 | 1.973 |
| Ironside | 2.513 | 2.529 |
| Rhino | 2.461 | 2.530 |
| Ring of Fire | 2.444 | 2.504 |
| Florida United | 2.441 | 2.177 |
| Condors | 2.401 | 1.530 |
| Sub Zero | 2.369 | 2.221 |
| Prairie Fire | 2.336 | 2.023 |
| PoNY | 2.291 | 2.569 |
| Chain Lightning | 2.156 | 1.980 |
| Temper | 1.996 | 2.252 |
| Tejas | 1.967 | 1.284 |
| GOAT | 1.965 | 2.709 |
| Floodwall | 1.955 | 1.228 |
| Streetgang | 1.930 | 1.632 |
| Galaxy Swag Universe | 1.923 | 1.490 |
| H.I.P. | 1.909 | 1.054 |
Women’s
1 bid: Great Lakes, Mid-Atlantic, and North Central
2 bids: South Central, Southeast, and Southwest
3 bids: Northwest
4 bids: Northeast
Compared to the actual bids assigned, the Bradley-Terry system results in no bid changes.
| Team | Rating | Strength of Schedule |
|---|---|---|
| Fury | 4.380 | 2.169 |
| Brute Squad | 4.263 | 2.143 |
| Riot | 4.243 | 2.415 |
| Molly Brown | 3.414 | 2.118 |
| Traffic | 2.892 | 2.482 |
| Iris | 2.788 | 1.329 |
| Scandal | 2.517 | 2.338 |
| Capitals | 2.503 | 1.832 |
| Ozone | 2.315 | 2.099 |
| Nightlock | 2.181 | 1.844 |
| Heist | 2.096 | 1.399 |
| Phoenix | 2.022 | 1.787 |
| Schwa | 1.995 | 1.975 |
| Showdown | 1.805 | 1.476 |
| Bent | 1.703 | 1.485 |
| Underground | 1.561 | 1.505 |
| Hot Metal | 1.459 | 0.894 |
| Green Means Go | 1.438 | 1.427 |
| Wildfire | 1.388 | 1.665 |
| Viva | 1.280 | 1.102 |
| Vintage | 1.256 | 0.852 |
| Rut-ro | 1.245 | 1.050 |
| Nemesis | 1.226 | 1.293 |
| Colorado Small Batch | 1.034 | 0.582 |
| LoCo | 1.026 | 0.623 |
Mixed
1 bid: Great Lakes, Mid-Atlantic, and Southeast
2 bids: Northwest and South Central
3 bids: North Central, Northeast, and Southwest 7.
Compared to the actual bids assigned by the USA Ultimate algorithm, the Bradley-Terry system would result in the following bid “changes”: MA: -1, NC +1, NE -1, SW +1
| Team | Rating | Strength of Schedule |
|---|---|---|
| The Chad Larson Experience | 3.424 | 2.071 |
| Slow White | 2.857 | 1.939 |
| Wild Card | 2.843 | 1.861 |
| Mischief | 2.835 | 1.900 |
| Drag’n Thrust | 2.780 | 1.768 |
| Seattle Mixtape | 2.646 | 1.975 |
| Polar Bears | 2.590 | 2.113 |
| Union | 2.477 | 2.334 |
| Bucket | 2.368 | 1.193 |
| Amp | 2.333 | 2.063 |
| Blackbird | 2.205 | 1.874 |
| Love Tractor | 2.164 | 1.424 |
| Metro North | 2.163 | 1.393 |
| Cosa Nostra | 2.126 | 2.115 |
| NOISE | 2.045 | 1.785 |
| Bessarion | 2.043 | 1.961 |
| Mental Toss Flycoons | 2.026 | 1.483 |
| Dorado | 1.952 | 1.315 |
| shame. | 1.928 | 1.380 |
| RUA | 1.921 | 1.415 |
| American BBQ | 1.914 | 1.721 |
| Steamboat | 1.903 | 2.110 |
| Minneapolis Millers | 1.894 | 1.404 |
| The Muffin Men | 1.883 | 1.110 |
| Ambiguous Grey | 1.873 | 1.306 |
Other Advantages to the Bradley-Terry System
Several related values can be calculated from the ratings, such as strength of schedule. Also, the probability of a winning any given game can be calculated from the probability of winning a single point8.
Expected point scores can also be calculated, along with expected point spreads. For example, Fury (rating 4.380) and Molly Brown (rating 3.414) would have the following probabilities of outcome:
| Fury Score | Molly Brown Score | Probability |
|---|---|---|
| Up to 11 | 15 | 10.98% |
| 12 | 15 | 4.02% |
| 13 | 15 | 4.69% |
| 14 | 14 | 12.03% (overtime) |
| 15 | 13 | 7.72% |
| 15 | 12 | 8.48% |
| 15 | 11 | 8.94% |
| 15 | 10 | 8.98% |
| 15 | 9 | 8.54% |
| 15 | 8 | 7.63% |
| 15 | Up to 7 | 17.99% |
Under this model, Fury is expected to win 75.7% of its games with Molly Brown, with an expected margin of victory of 3.1.
Any model will have caveats. This one is no different. Each point is assumed to be played identically. There’s no consideration of offensive and defensive lines, team depth, or cap limits. If only considering effects on winning an overall game, trading points and offensive/defensive lines will serve to reduce variance and decrease the probability of a potential upset.
Capping a game and reducing its length will increase the probability of an upset.9 Of course, many of these limitations apply to the USAU algorithm as well.
The main advantage this system has over the USAU algorithm is a team rating conveys additional information about the expected outcome of a game. As shown above, win percentage and point spreads can be calculated. Also, the USAU algorithm has been shown to provide a disproportionate benefit to defeating a similarly rated team. Under the Bradley-Terry model, playing a close game against a similarly rated team will not greatly affect either team’s rating.10
If you are interested in an even more technical discussion, here is the full research paper.
Stephen Wang was immensely helpful in discussions I had with him. He suggested that I treat each point as a “mini-game”, and also steered me towards using numerical methods rather than trying to invert an enormous matrix.
There are several unofficial rankings algorithms in use for college hockey, but I took one (the Bradley-Terry system) that I find the most interesting and applied it to ultimate. ↩
See this writeup on the NCAA website for more information about the college hockey selection process. ↩
There’s several ways to determine exactly how much it should be adjusted, but I used Newton’s method for ease. ↩
In calculating the ratings adjustment for Newton’s method, I only considered the derivative of a team’s rating and win total with respect to its own rating, and ignored the differential effect of adjusting opposing teams’ ratings. ↩
less than 0.0000001 for any team in the ratings. ↩
Data was scraped off the USAU website, so some data may be included / excluded that was not used in the “official” USAU calculation. ↩
Excluding Union and Bessarion for the NE — including them would give the NE 4 bids and the NW 1 bid ↩
using a modified binomial distribution ↩
The details drawn from the model are likely skewed as well. The probability of a blowout win is likely overstated. Teams may have a more open rotation in such a scenario in order to rest starting players. Team depth would become more of a factor, and explicitly accounting for team depth is not done in this model. ↩
I haven’t done a full analysis on the effects of playing a higher/lower rated opponent on a team’s rating, but I don’t think it will affect it because, unlike the USAU system, the winner does not get an automatic +125 points. ↩